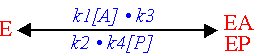About Enzyme Reaction Mechanism Database
[ERM Main Menu]
[About the ERM]
[Cleland notation]
[Enzyme kinetics]
[Alternate nomenclature]
[Publication]
Inline with rapidly growing information on genome and cellular function metabolic
models become very useful tool for understanding cellular life.
To help researches to create a wide range of metabolic models the ERM database has
been created. It is a part of EMP_project
(Selkov E. E. et., Nucleic Acids Res., 1996, v. 24(1), pp. 26-28)
and was initiated by Laboratory Metabolic Simulation and Bioinformatics of the
Institute of Theoretical and Experimental Biophysics of the Russian Academy of
Sciences, Pushchino, Moscow Region, Russia, headed by Professor Evgeni E. Selkov.
Currently ERM represents data on more than 90 reaction mechanisms catalyzed
by single active site enzyme and covers most of one, two, three, four substrates/products
and different inhibition types mechanisms. One record of ERM contains information of
enzyme reaction mechanism in Modified Cleland notation.
The ERM format has 8 main fields that may be presented as structure:
kinetic scheme
reaction graph
stoichiometric matrix
mathematical model
rate law
lumped rate law and kinetic constants
dimensionless rate law
references
Kinetic scheme
The following way of enzyme reaction mechanisms representation is offered by Cleland:
the various enzyme forms are written below than horizontal line, and arrows designate
the substrates connection or products release. Going along the scheme left to right
and adhering the specified direction of arrows, we receive forward reaction,
and on the contrary for the reverse reaction.
The rate constants are written on the left and right of arrows. k1,k3,...,
and so on are the rate constants in the forward direction, and k2,k4,...,
and so on - in the reverse direction.
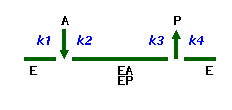
Example: (Uni Uni Mechanism)
or
Elementary Reactions
| A + E |

k1 |
EA |
| EA |

k2 |
A + E |
| EP |

k3 |
P + E |
| P + E |

k4 |
EP |
|
Rapid Exchange
| EA |
 |
EP |
|
[Return to Top]
Reaction graph
This is a scheme for the enzymological reaction connecting the reactant concentration by arrows,
showing the direction and the rate of the transition. The graph is equivalent to the system
of equations presented the enzyme reaction mechanism and its solution gives the solution
for this system. The solution of the grapf does not need special mathematics; it lends itself
to graphical analysis according simple rules.
Example: (Uni Uni Mechanism)

or
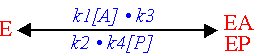
[Return to Top]
Stoichiometric matrix
The elements of matrix are the numbers (a stoichiometric multipliers M) determining
the quantity of metabolit molecules that participates in the stoichiomeric equation.
If M>0 or M<0 the metabolit are the product or the substrate respectively and in case
M=0 the substance don't attends in the reaction. Row is the reaction metabolite,
string - the elementary step reaction.
Example: (Uni Uni Mechanism)
| RI | E | A | P | EA |
| R1 | -1 | -1 | 0 | 1 |
| R2 | 1 | 1 | 0 | -1 |
| R3 | 1 | 0 | 1 | -1 |
| R4 | -1 | 0 | -1 | 1 |
[Return to Top]
Mathematical model
All mathematical models of enzymatic reactions are derived as an ordinary differential
equation (ODE) model from a stoichiometric matrix by using
DBSolve package.
Example: (Uni Uni Mechanism)
x[3] = x[1]-x[2]+1.0
x[4] = -x[1]+2.0
F[1] = -v[1]+v[2]+v[3]-v[4]
V = v[3] - v[4]
Where:
E = x[1]
A = x[2]
P = x[3]
EA = x[4]
Et = E + EA
v[1] = k1*A*E
v[2] = k2*EA
v[3] = k3*EA
v[4] = k4*P*E
[Return to Top]
Rate law
The steady-state rate equation for the full reversible reaction be written in
several forms. The form obtained by the simple and elegant method of King and Altman
(King E. L., Altman C. A., J. Phys. Chem., 1956, v. 60, p. 1375-1378)
and method of graph of Volkenstein and Goldstein (Volkenstein M. V., Goldstein B. N.,
Biochem. Biophys. Acta, 1966, v. 115, p. 471-477). This methods allows the steady-state
rate equation for mechanism of considerable complexity to be written down in terms of
the individual rate constants without going through messy algebraic expansions of large
determinants.
Example: (Uni Uni Mechanism)
VE = NE / DE
NE = Et*(k1*k3*A - k2*k4*P)
DE = CON + C1 + C2
CON = k2 + k3
C1 = k1*A
C2 = k4*P
[Return to Top]
Lumped rate law and kinetic constants
In this field we presents the steady-state rate equation in the kinetic constant terms
derived by using Cleland's elegant approach and modified
nomenclature. Cleland's approach show how rate equation expressed in terms of rate
constants can be transformed into equation expressed entirely in terms of measurable kinetic
constants.
Example: (Uni Uni Mechanism)
VK = NK / DK
NK = V1*V2*(A - P/Keq)
DK = CONST + C01 + C02
CONST=Ka*V2
C01=V2*A
C02=V1*P/Keq
Maximal velocities for both directions:
V1 = k3*Et
V2 = k2*Et
Michaelis constants:
Ka = (k2+k3)/k1
Kp = (k2+k3)/k4
Equilibrium constant:
Keq = k1*k3/(k2*k4) or
Keq = (V1*Kp)/(V2*Ka)
[Return to Top]
Dimensionless rate law
In many cases to the researchers is conveniently to use the rate equations containing
dimensionless parameters. This field exists for this purpose.
Example: (Uni Uni Mechanism)
VD = ND / DD
ND = Sigma - HI*Ro
DD = 1 + Sigma + Ro
Sigma = A/Ka
Ro = P/Kp
HI = V2/V1
[Return to Top]
References
This field contains the links to corresponding records in:
bibliographic database PubMed,
metabolic reconstruction tools WIT,
Kyoto University Ligand Chemical Database KEGG,
factografic databases EMP Project and
MPW,
Enzyme Nomenclature database,
nucleotide and amino acid sequence database SWISS-PROT,
Protein Database PDB.
Example: (Uni Uni Mechanism)
here.
[Return to Top]
[ERM Main Menu]
[About the ERM]
[Cleland notation]
[Enzyme kinetics]
[Alternate nomenclature]
[Publication]
Russian Academy of Science
Institute of Theoretical and Experimental Biophysics
Laboratory of Metabolic Simulation and Bioinformatics
Pushchino, Moscow reg., Russia, 142290.
Created by Milya Galimova.